志賀浩二先生の訃報に接し,30講シリーズを改めて眺めてみようと思う。で,シリーズ最初の『微分・積分』。〈数と数直線〉という初歩的なところから始めて,テイラー展開とそのもつ深淵な意味合いを感じさせるところまで持っていってくれる。Tee Timeで述べられる志賀先生の思想もまた面白い。さらに最後には,このあとの展開として関数論の世界へ誘ってくれる。関数論,面白そうだな,と思った。
1. 数と数直線
微積分の話をするためには,さらに実数まで数の範囲を広げる必要がある。しかし有理数では,四則演算は自由にできるのだから,自然数から有理数まで数の範囲を広げてきたような考えで,もう有理数を広げるわけにはいかない。どのような考えに立って,有理数の範囲をさらに広げて実数という新しい数の範囲に到達するか,それは次の講の主題である。
2. 数直線と実数
有理数は,有限小数か,循環する無限小数で表わされる数である。
循環しない無限小数として表わされる数を無理数という。
有理数と無理数を合わせて実数という。したがって実数は,有限小数または無限小数として表わされる数である。
有理数は四則演算で閉じていた。有理数から実数へ数の世界を広げる本当の必要性は何だったのだろうか。
有理数から実数まで数の範囲を広げておかないと,数の世界の中でこの確かと思われる認識の保証は得られなかったのである。
数学の用語では,近づくはずの点列のことを,コーシー列という。この用語を使えば実数は,すべてのコーシー列がある点に近づくことを保証する数の世界である。
3. 座標と直線の式
4. 2次関数とグラフ
5. 2次関数の最大,最小
質問 接線の傾きの話は,大体理解できたように思いましたが,一つ不安な感じが残りました。それは,動点QがどんどんPに近づいていって,最後にQがPにできなくなるのではないかということです。
答 この質問は極限概念に関することであって,これからしだいに明らかにしていくつもりである。
6. 3次関数
7. 3次関数と微分
8. 3次関数のグラフ
9. 多項式関数の微分
10. 有理関数と簡単な無理関数の微分
質問 有理関数のグラフについて,上の説明を聞いて思ったのですが,有理関数のグラフが波打つ場所は有限個ですから,どこまでも波打つような図55のようなグラフは,有理関数では絶対表わせないのでしょうか。
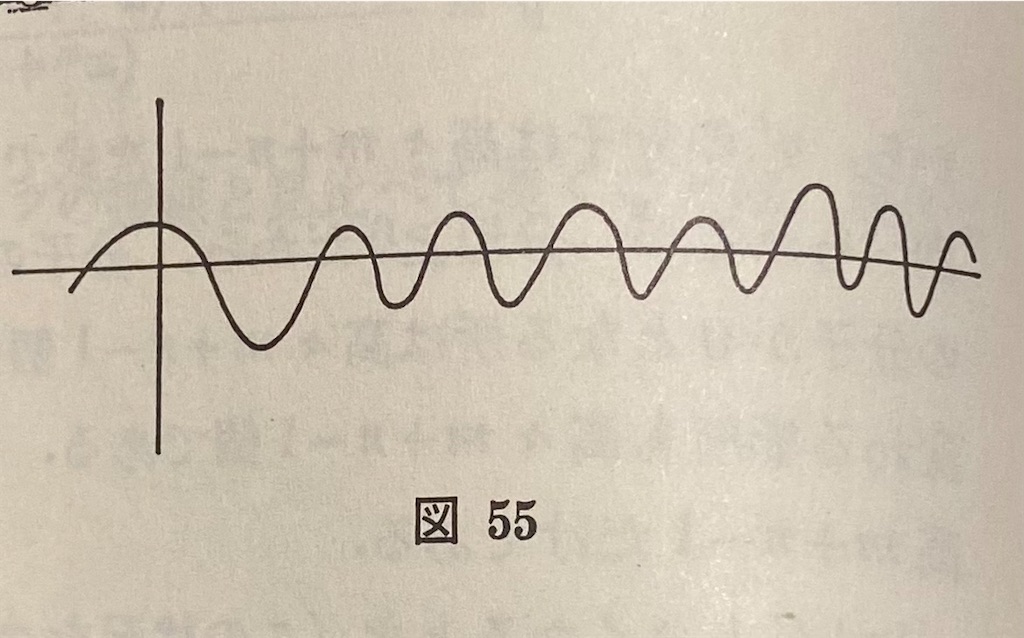
答 その通りである。自然現象の観測などから現われる関数の中で,有理関数でまわされるようなものは,ごく特別なものに限られる。これからは,有理関数では表わせない関数の中で,最も基本的な,三角関数,指数関数,対数関数などについて,微分の性質を調べていきたい。
11. 三角関数
12. 三角関数の微分
13. 指数関数と対数関数
y = exという関数は,微分して導関数をとっても,もとと変わらない関数である。このような性質をもつ関数は,exか,あるいは,e=xを何倍かした関数,すなわち Cexという関数しかないことが知られている。
14. 合成関数と微分と逆関数の微分
微分は,関数のグラフを解析する最も重要な手段である。もしこの手取が,関数の複雑さに比例して難しくなったり,グラフの概形を知らなければ計算できないようなものだったら,これほど広く,有効に使われることはなかったろう。微分の計算は,なれれば誰にでもすぐできる。ここに微分の働きが,数学を超えて,広い分野にまで浸透していった1つの理由がある。‘微分する’という‘演算’が,関数の複雑さにかかわらず,比較的簡単にできる理由は,微分が関数の各点ごとのごく近くの性質にしかよらないからであって,実際,各点ごとで関数を微分するには,グラフが複雑な様子で広がっていくさまを,全部見通さなくてもよいのである。
15. 逆三角関数の微分
逆三角関数の導関数は,三角関数の導関数と比べてみると,大分様子が違っていることに気がつく。三角関数の導関数は,すべてまた三角関数で表わされていた。それに反し,逆三角関数の導関数は,もう三角関数ではなくて,無理関数や,有理関数になっている。
もっとも同様な状況は,logでの導関数にも起きている。
グラフの上では,もとの関数と逆関数のグラフは,y=xという直線に関して対称な形をとっているにすぎないのに,導関数の上では,このようなはっきりとした違いが生じてくる。これは,一種の‘解析の魔術’とでもいうべきものであろう。
16. 不定積分
質問 たし算よりは,その逆演算である引き算の方が難しかったし,掛け算よりは,その逆演算である割り算の方が難しかったと思います。微分よりは,不定積分を求める方が,やはりずっと難しいことなのでしょうか。
答 冗談のようないい方をすれば,一般的には,生むことよりは,生みの親を見つける方が難しい。微分するとは,関数fから,新しい関数f'を生むことであった。それに反し,積分では,与えられた関数fに対してF'=fとなる関数Fを求めることを問題とするが,このようなFがあるかないかーーfを生んだ親がいるのか,いないのかーーが,すでにはっきりしないことがある。
しかし,今度は存在したとしても,その関数Fが,有理関数や三角関数や指数関数などを使ってかき表わされる関数なのかどうかーー生みの親は,私達があだんつき合っている範囲の中の人なのかどうかーーということが,別の新しい問題となってくる。このことについては,昔から多くの研究があるが,一般的な理論は難しくて,専門家以外には,深い霧の中にあるといってよい。
17. 不定積分の公式
18. グラフのつくる図形の面積
私達がここで取り扱う関数は,それほど複雑なものではないので,そのグラフのつくる図形Sはすべて面積をもっている。もう少しはっきりとしたいい方で述べれば,連続関数のグラフのつくる図形Sは,必ず面積をもっている。/これからは,面積というときには,いままで述べてきたような。グラフを挟む階段状の図形の面積の極限の値として考えることにする。
19. 定積分
ライプニッツという数学者は,‘数学の秘密はその記号にあり’という言葉を残していることからもわかるように,数学における記号のもつ意味をよく知っていた。
20. 定積分と不定積分
この基本定理の示していることは,上の例でも示したように,関数のグラフがつくる図形の面積ーー定積分ーーを,微分の逆演算ーー不定積分ーーによって求めることができるということである。
定積分を生んだ母胎は,面積の考えである。一方,不定分を生んだ母は,微分の概念であって,それはさかのぼれば,グラフの1点における接線の傾きである・グラフの面積は,関数の大域的(global)な挙動にかかわっている。それに反し,微分は,関数の局所的(local)な性質だけに注目している。微分・積分法の基本公式は,関数のこのような大域的な様相と,局所的な様相とが,この公式によって結ばれていることを示している。
また,面積の考えは,エジプトの測量術にまでその源をたどれるような,古くからあった基本的な考えである。しかし,与えられた面積を具体的に計算することは,非常に難しい問題であった。他方,不定積分は,微分の逆演算として比較的計算は簡単であるが,グラフの性質と,どのように関係しているかは,あまり明らかなことではなかった。すなわち,定積分の考えは,明快であるが,計算しにくく,不定積分の方は計算はしやすいが,そのグラフに対する意味は,判然としなかった。微分・積分法の基本公式は,いわばそれぞれのもつ長所と短所を,互いに補うような形で,2つのものを等号で結んでいる。
この定理のもつ意味は,まことに深いものがある。
21. 円の面積と球の体積
22. 関数の例
この講は,幕間のような講であって,いくつかの関数の例を示すことにより,関数概念をもう少し豊かなものとしたいという意図をもっている。
23. 極限概念について
もちろん,あるものが何かに近づくという感じは,私達の空間,時間の中の行動の中にあって,はっきりと把えられるものだから,‘近づく’という感じから出発した推論が誤りを導くということは,ふつうはあまりないのである。しかし,数学が無限級数とか,複雑な関数を微分したり,積分したりするようになってくると,‘近づく’という概念を明確に定義しなくては間違った推論に導くということも起きてくる。これを正す必要もあって,ε-δ論法は前世紀の半ば頃から登場してきたものである。
その証明を見てもわかるように,ε-δ式の極限の表現法は,私達の近づくという感覚と数学の形式を融和させる一つのかけ橋としての役目も果しているのである。
24. 極限の公式と連続関数
(I),(III)の上のような証明が,ε-δ論法といわれるものであるが,このような論法を強調すると。微分・教分への関心を減じさせることにもなりかねない。読者は,証明の大体の輪郭を理解すればよいのであって,むしろここでは,‘近づく’という感覚的なものが,ε-δ式の定式化を通して,数字の加法とか乗法の演算に,いかになじんでくるかに意をはらってほしいのである
極限の公式を見て思ったのですが,関数を微分するときには,f(x+h) - f(x)と,hで割るという演算が主で,これは四則演算です。第1講,第2講での話を思い出してみると,それならば微積分は,有理数の範囲でできたのではないかと思いました。微積分を展開するために実数が必要であった理由はどこにあったのでしょうか。
微積分を支える世界は,有限の量を四則演算して得られる世界だけではなくて,極限操作へと移っていって得られる,いわば無限の世界である。したがって,微積分という学問の体系が成り立つためには,極限操作が自由にできるような数の世界,第2講でのいい方にならえば,近づくはずの数列(コーシー列!)が,必ず極限値をもつような数の世界を設定しておくことが必要だったのである。実数はその要求を満たす数の体系であった。
25. 平均値の定理
大体,どの散分の数科書を広げてみても,ロルの定理は比較的中心的な場所におかれていて,その重要性を暗示する形をとっている。しかし,どうしてロルの定理のような簡明な定理が,微分学にとってそんなに重要なのだろうか。
それを知るには,微分の最初の出発点に戻って考えてみるとよい。微分は,1点のごく近くのグラフの模様を,接線の傾き具合におき換えて,グラフの様子を調べようとする。しかし,局所的な様子をいくら詳しく調べてみても。グラフが大域的につながっていく模様は,原理的にはわからぬことだろう。
‘微分’という考えが,効果的に,いろいろな問題の解決へと働いていくためには,この微分のもつ‘局所性’を‘大域的’なものへと変えていく転回点が必要である。この転回点の,最初の最も基本的な形がロルの定理によって与えられている。ロルの定理の条件f(a) = f(b) = 0は,aとbとがいくら離れていてもよいのだから,大域的な条件である。この大域的な条件から,微分に関するある性質が導かれていく点が重要なのである。
26. 平均値の定理とその拡張
27. テイラーの定理
テイラーの定理で,特にa = 0の場合を,マクローランの定理といって引用することが多い。
このような発見的推論によって,マクローランの公式の意味するものが,多少とも明らかとなるという長所はある。数学では,多くの場合。発見的推論がまずあって,次にそれをいかに論証するかというように,進んでいるようである。発見的推論という考え方は,もっと尊重されてもよいのではなかろうか。
28. テイラーの展開
29. テイラーの展開(つづき)
テイラー展開(1)の左辺は,関数が広がっていく模様を示し。右辺は,高階微分という考えを用いて,原点のごく近くのf(x)の情報を,できるだけ取り出したものとなっている。左辺は,関数fの大域的な性質であり,右辺は局所的な性質である。この2つの相反する性質が,関数fでは,完全に結び合っているということを主張するのが,テイラー展開の意味である。
前講でさりげなくかかれている剰余項が0に収束する条件は,まことに強い条件をf(x)に課していることがわかる。
質問 テイラー展開ができるような関数は,むしろ例外的なものだということはよくわかりました。しかしなぜ,この例外的な関数の方に,私達がらだんよく使っており,また自然現象の数学的記述の中にもふつうにでてくる,exやsin x,cos x,などが含まれていたのでしょうか。
答 理由はわからない。God knows というべきであろう。しかし,テイラー展開のような定式化によって,関数のもつ大域的な性質と,局所的な性質がはっきりと表現できたことは,まことに驚くべきことであった。大域的な観点と局所的な観点の織りなす機は,微積分全体の中を流れる基調のようなものであるが,この調べは,どこかでニュートン力学の因果法則の調べと,重なり合っているようである。
30. ウォリスの公式
質問 これからどんなことを勉強したらよいのでしょうか。
答 この30講で述べてきたことは,ごく基本的なことで,カ学への応用とか,最大,最小のいろいろな問題なども取り扱うことができなかった。微分には,実に多種,多様な問題がある。微積分に一層近づくためには,これらの問題を解く力を養成することが必要となってくるだろう。
また,微分方程式や,多変数の微積分についてもほとんど一言も触れることができなかった。これらは,また新しく勉強する主題となるだろう。テイラー展開によって表わされる関数ーー解析関数ーーの性質をよりよく理解するためには,数の範囲をさらに実数から複素数へと広げなくてはならない。そこには関数論の透明な理論が展開している。
ここでの勉強が,微積分を身近に感じさせ,さらにもう少し数学を学んでみようかという気持を起こさせたならば,嬉しいことである。
31. 問題の解答
32. 索 引
微分・積分30講 (数学30講シリーズ ; 1) | NDLサーチ | 国立国会図書館
413.3
